はじめに ― この記事の立ち位置について

はじめに ― この記事の立ち位置について

本書は、一人のコンサルタントが歩んできた実績や体験を単に記録するものではない。
また、最新のAI技術を解説するための技術書でもなければ、経営論を体系的に整理した教科書でもない。
本書は、それらのすべてを横断し、なおかつ超えたところに位置づけられる。

ここに描かれているのは、「企業が成長するとはどういうことか」を追い求めた軌跡であり、同時に「成長を再現するための方程式」を発見するまでの物語である。
それは、著者が大学の研究室から始めたデータ分析の試みから、大企業の経営会議で数百億円単位の意思決定を支える経験、そして社会全体を見渡す思想に至るまで、二十年近い試行錯誤の果てに結晶化した知見の集大成である。

技術書ではなく、物語である理由

AIやデータサイエンスを扱った専門書は数多く存在する。
だが、技術そのものを知っても、経営の現場で活かせるかどうかは別問題である。
経営者が最も知りたいのは「この技術で自社がどう変わるのか」、部課長が求めているのは「現場を壊さずに成果を出せるのか」、投資家が見ているのは「数字として再現性のある成長が描けるのか」である。

そうした問いに真正面から答えるためには、単なる理論や手法の解説では足りない。
必要なのは、「現場でどう起きたか」を描いた物語であり、読者が自らの企業に重ね合わせられるリアリティである。
本書が小説のような構成をとっているのはそのためだ。

成功譚ではなく、普遍原則を掘り起こす書

本書に登場する事例は、すべて実際の現場で生まれた成果や苦悩に基づいている。
通信業界での数千億円規模の投資評価、金融業界での数十億円単位の不正検知、製造業での赤字案件ゼロ化――これらは「華やかな成功譚」として並べることもできるだろう。
だが、本書の目的はそこにない。

むしろ、本書は「なぜ成功したのか」「なぜ失敗しなかったのか」「どうすれば他社でも再現できるのか」を徹底的に掘り下げる。
その過程で浮かび上がるのは、業界や規模を問わず通用する普遍原則である。
著者自身の経験を超え、あらゆる企業が手にできる「成長の方程式」として結晶化させることを意図している。

読者に向けられた三つの視点

この本は、読者を特定の一つの立場に限定しない。
むしろ、三つの層に対して同時に語りかける。

1. 経営層へ ― 「不確実な時代に、意思決定をどう支えるか」
   
   
2. 部課長へ ― 「現場を守りながら、どう成果を出すか」
   
   
3. 投資家へ ― 「資本をどこに投じれば、確実に成長を生むのか」
   
   

これら三者に共通するものは「成長への渇望」である。
その渇望を満たす方法論こそが、AIDグロースメソッド（AID＝AI-DataScience）であり、本書の核にある。

兆円企業を見据えた物語

さらに言えば、本書は単なる企業改善の指南書でもない。
著者が目指すのは、数百億円・数千億円規模の成果を超えて、兆円単位の社会的インパクトを持つ企業を育てることだ。
「兆円企業」というビジョンは誇大妄想ではなく、再現性ある成長の方程式があればこそ描ける現実的な未来図である。

その未来に向けて、経営層も部課長も投資家も、そして読者自身もまた、この物語の登場人物となる。

本書の立ち位置

したがって本書は、以下の三つを兼ね備える稀有な書物である。

• 物語でありながら経営書
  
  
• 事例集でありながら方法論
  
  
• 個人の体験記でありながら社会への提言
  
  

読者はこの本を読み進める中で、自分の立場に応じたメッセージを受け取ることになるだろう。
経営者は未来の投資判断の武器を、部課長は現場を動かすヒントを、投資家は資本を安心して託せる論拠を。

この本は、「AIで企業は変わるのか」という問いに答えるものではない。
答えはもっと単純だ。
「AIを正しく使う意思を持つ企業が、自らを変える」
本書はその意思を持った企業の伴走者であり、読者自身が次の物語を描くための出発点である。

これが、本書の立ち位置である。

創業の動機とプロダクト化

当ベンチャーの創業者は、AIとデータで企業の成長を支えてきた現場の中で、アートを通じて創造力に目覚めた。そこで得た気づきをもとに、現場で通用した成功メソッドを誰もが使える“方程式”としてプロダクト化し、産業横断で再現できる形へと発展させた。社会全体のAI／デジタル活用を一段進化させることを使命とし、このAIベンチャーを創業した。本書は、その設計思想と実装の記録である。

彼はアートの創作活動を通じて、ひとつの作品を生み出す過程が“量産”の思考へとつながることに気づいた。絵を描くたびに試行錯誤を繰り返し、同じ技法を別の作品に応用できる。その体験が、企業成長のメソッドをプロダクトとして次々と形にする発想へと直結した。単発の成果を超えて、再現可能な仕組みを量産して社会を進化させることこそが、彼の使命だと確信した。スティーブ・ジョブズと多数の共通点があることも、ひとつの理由かもしれない。

	当ベンチャーの創業者	スティーブ・ジョブズ
誕生日	2月24日	2月24日
血液型	O型	O型
アート	油絵	カリグラフィー
宗教／哲学	浄土真宗	禅
事業	AI/データ ✕ 創造性	テクノロジー ✕ リベラルアーツ

コロナ陽性者数に正規関数を当てはめた推測の評価2

推定を作ってから約２ヶ月経ってからのコロナ陽性者数の推測結果、以下になりました。

第５波までの傾向だったらもう収束しているはずですが、収束しておらず、１日6,000〜7,000人くらいで停滞している感じです。これくらいの陽性者数が底になっている印象。恐らく、これからは今までと違う動きをすると思われるので、また違う推測モデルが必要かも。

コロナ陽性者数に正規関数を当てはめた推測の評価

2/6に、↓の記事で東京都のコロナ陽性者数に正規関数を当てはめて推移を予測しました。1ヶ月ほど経ったので、その予測の評価をしてみました。

iisssseeiiii.hatenablog.com

評価した結果は次の図のようになりました。

オレンジ線が実際の陽性者数で、青破線が2/6までのデータを使ったモデルで推測した値です。モデルを作ってから少し陽性者数が増加し、推測ではもっと増えると計算されてましたが、そこまで増えませんでした。ただ、その後の減り方は緩やかだったので、3/14時点では正規曲線の値に近づいています。

この後どうなっていくか分かりませんが、モデルだと4/10あたりで収束になっています。ただ実際のオレンジ線はゆっくり減ってくように見えるので、収束はもっと遅い可能性もあります。

2月の中旬くらい、モデルほど実数が増えなかった原因としては、個人的な感想ですが、感染者数に検査が追いついてなかったのではと思ったり、みなし陽性で実際の陽性者より少なく報告されてるなどあるのかなと思ったりしています。何かエビデンスがあるわけでないので、純粋な個人的感想です。

1/4あたりに第6波が始まり、2/6までの1ヶ月くらいのデータで計算したモデルですが、全く外れてるというわけではない感じがします。流行の周期自体もだいたい3ヶ月くらい。なぜかは分かりませんが、集団行動とか免疫とかが関係しているのかな、？4月上旬あたり、収束しているといいです。

計算上の最適とビジネス上の最適の違いについて

AI、機械学習、データサイエンスでモデルを作って分析したり予測するとき、モデルをどう作ればいいか？という問題で。

学問的には、交差検証(クロスバリデーション)をしたり、何らかの当てはまり指標を最適化してモデルを作ったりすることが望ましいとされます。

が、自分がこれまでデータをビジネス実績に結びつけてきた実感としては、そうやってつくったモデルは役に立たないことが多い。

全体的に、保守的なモデルになり、業務知見と同じような結果で、モデル使う必要ない、データでは何も見つからないね、となってしまうことが多い。業務知見を超える知見は、最適なモデルより"少し過学習気味"に設定したときに現れてるように思っています。

自分が新規のデータを分析するときは、だいたい決定木を試してみるが、わざと過学習気味の木を作る。そしてそれをビジネス側に説明しながら、実際の業務でどう活用できるかを詰めていく。

決定木の場合で言うと、枝の2〜3段目くらいまでは業務知見で説明が付く事が多い。さらに分岐させていくと、業務知見ではカバーできてなかった細かいルールになっていく。そのルールが、ほんとうに法則を表しているのか、それともたまたまの過学習なのか。それは最適化の計算結果で判断するのではなく、ビジネス側と議論してお互い一緒に考える。

最終的には、実際に使ってみないとそのルールが正しいかどうかは判断できないので、間違っているかもしれないということを念頭におきながら、試せる範囲内で実証実験をしていく。それが、最速で最大限に分析結果をビジネス成果に繋げることができる方法かなと。

データを活用して実際のビジネス収益を上げられるかどうかは、計算上の最適解よりももう少し深いところの特徴が有効なものかどうか次第かなと感じます。

コロナ陽性者数の推移への正規関数の当てはめ

コロナの感染者数の推移に関して、感染拡大が上がって下がる変化の仕方を関数で表現できないか、またそれによってある程度拡大は収束の推測ができないかと思っていました。自分が知っている関数の中では、正規分布の確率関数が、拡大と収束の形に一番近いため、正規関数に当てはめて分析してみました。

※この取り組みは、私個人の見解で行っているものであり、また厳密な研究をしているわけではないので、必ずしも正解というわけではなく、あくまでも参考例として捉えてもらえればと思います。

結果的にいうと、正規関数のあてはまりは悪くなく、一定程度の参考になりそうかなというものです。東京の感染者数に対して、いま感染拡大している第６波に当てはめてみると、第６波が始まってから52日程度（2/24あたり）がピークで、７日平均が3.5万人程度という計算になっています（本記事一番下↓の図参考）。７日平均が約3.5万人なので、曜日ピークの水・木曜あたりは4〜5万人くらい？→パラメータを追加して分析したら47日後（2/19あたり）に約2.7万人という結果に

ただこの計算も、この１週間で結構ぶれているので、また数日や１週間程度したら大きく変わるかもしれません。第６波とみられる日から21日間のデータを使って計算したピーク人数は約6.6万人、28日間のデータを使ったピーク人数は約3.3万人と大きく減少しました。この１週間くらい、増加スピードが緩やかになっている影響かと思います。

今回行った計算は、”増えだしてからx日間のデータを使って正規関数を当てはめ、もっとも当てはまりがいいパラメータを選択する”、というものです。この方法を東京の第４波と第５波のデータに当てはめてみたところ、そこそこ当てはまりが良かったです。第４波のときは実際のピークが935人（過去7日間の平均）であるのに対し、推定値が961人〜1,022人。第５波のときは4,923人（同上）であるのに対し、4024人〜7,347人（35〜42日の間で拡大スピードが少し下がった）でした。

この方法が、全国のデータで通用するのか、また世界各国のデータで通用するのかは未確認です。下記、Rで行ったプログラムと、結果の一部です。データは、下記の東京都のオープンデータから取得したcsvを利用しています。

データ取得元：東京都 新型コロナウイルス陽性患者発表詳細 - 東京都_新型コロナウイルス陽性患者発表詳細（全期間一括版） - 東京都オープンデータカタログサイト

■第４波を2021/3/18〜6/18としてデータを作成したときの結果。

・3/18から21日（3週間）のデータを使って計算した結果

縦軸↑：7日平均感染者数
横軸→：開始日からの日数（このグラフは3/18が1、50の時点は5/6）
丸：観測された値
青丸：計算に使ったデータ
黒丸：その後実際に観測されたデータ
曲線：計算した正規関数

・3/18から56日（8週間）のデータを使って計算した結果

■第５波を2021/7/5〜10/6としてデータを作成したときの結果。

・21日間のデータを利用

・28日間のデータを利用（この時点ではピークが大きく計算されている）

・35日間のデータを利用（28〜35日間の拡大が少なかったためか、ピークも小さくなった）

・70日間のデータを利用（若干当てはまりが悪く見える。正規関数でなく、歪正規関数のように、他の関数の方が当てはまりがいいのかもしれない）

■第６波を2022/1/4〜としてデータを作成したときの結果。最大で2/5までの33日間のデータを利用。

・21日間のデータを利用

・28日間のデータを利用（感染者が急に増えたためか、ピークが約6.6万人と計算）

・33日間のデータを利用（この１週間くらいは感染拡大が鈍化したためか、ピークが約3.5万人に下がる。2/24日あたりをピークに減少に向かう？拡大の鈍化が続けば、ピークの人数ももっと減るかも）

↓追記：パラメータ追加して計算するとピークまでの日数とピーク人数が減少（2/19あたりがピーク、７日間平均が約2.7万人、水・木のピークだと3.5〜4万人くらい？）。

上に書いたように、本記事は正確な研究に基づいたものではないですし、流行学的な感染モデルのようなものを仮定したりしているわけではありません。ただ観測された感染者数だけを使って計算しています。今後の個々人の行動や政策などによって大いに変わる可能性はありますが、ある程度の参考や目安になればと思っています。

Data <- read.csv(".../130001_tokyo_covid19_patients.csv", as.is=T)

table(Data$発症_年月日)

Kansensha <- table(Data$公表_年月日)

#  7日間移動平均を利用→正規関数のブレが少なくなった
Kansensha2 <- filter(Kansensha, rep(1, 7))/7


plot(Kansensha)
plot(Kansensh2)


Prm <- NULL

#  調査するパラメータの設定。当てはまりが良さそうな値の周辺を設定している
#  他の地域や時期を分析するときにはパラメータが大きく変わる可能性はある
peak <- c(100, 200, 300, 500, 1000, 3000, 5000, 10000, 30000, 50000)
mean <- c(45, 49, 50, 51, 52, 53, 55)
sigma <- c(0.05, 0.054, 0.055, 0.056, 0.057, 0.058, 0.059, 0.06)

for(a in 1:length(peak)){
  for(b in 1:length(mean)){
    for(c in 1:length(sigma)){
      Prm <- rbind(Prm, c(peak[a], mean[b], sigma[c]))
    }
  }
}

head(Prm)
dim(Prm)


Ryukou4 <- Kansensha[391:483]
Ryukou5 <- Kansensha[500:593]
Ryukou6 <- Kansensha[683:714]

R <- Ryukou3

Len <- length(R)
Len <- 40



Est <- function(R, Len){
  
  # base <- mean(R[1:7])
  base <- min(R[1:7])
  Ryukou <- R - base
  
  SDS <- NULL
  
  # i <- 1
  
  for(i in 1:nrow(Prm)){
    DS <- NULL
  
    for(x in 1:Len){
      peak <- Prm[i, 1]
      mean <- Prm[i, 2]
      sigma <- Prm[i, 3]
      
      # sigmaが小さい方が分布の幅が大きくなる結果になったので、式のプラスマイナスや分母が間違ってる可能性？
      # ただ、yを計算してプロットしたら当てはまりの良い正規分布になっているので、結果には問題なさそう
      DS <- c(DS, (Ryukou[x] - peak * 1/(2*pi*sigma^2)^0.5 * exp(- (x - mean)^2 / 2*sigma^2))^2)
    }
    
    SDS <- c(SDS, sum(DS))
    # print(i)
  }

  # SDS
  
  print(min(SDS))
  print(Prm[(SDS == min(SDS)), ])
  
  print(max(R))
  
  
  x <- 1:(length(Ryukou)+100)
  
  prm <- Prm[(SDS == min(SDS)), ]
  peak <- as.numeric(prm[1])
  mean <- as.numeric(prm[2])
  sigma <- as.numeric(prm[3])

  # sigma <- 0.1
  # peak <- 200
  
  y <- base + peak * 1/(2*pi*sigma^2)^0.5 * exp(- (x - mean)^2 / 2*sigma^2)
  print(max(y))
  
  
  plot(R, ylim=c(0, max(y*1.1)), xlim=c(0, max(x)))
  points(R[1:Len], col="blue")
  lines(y)
  
  y
}



Ryukou4.2 <- Kansensha2[391:483]
Ryukou5.2 <- Kansensha2[500:593]
Ryukou6.2 <- Kansensha2[683:715]



Est(Ryukou4, 21)
Est(Ryukou4, 35)
Est(Ryukou4, 42)

y4.2.21 <- Est(Ryukou4.2, 21)
y4.2.35 <- Est(Ryukou4.2, 35)
y4.2.42 <- Est(Ryukou4.2, 42)
y4.2.49 <- Est(Ryukou4.2, 49)
y4.2.56 <- Est(Ryukou4.2, 56)
y4.2.63 <- Est(Ryukou4.2, 63)
y4.2.70 <- Est(Ryukou4.2, 70)

y5.2.21 <- Est(Ryukou5.2, 21)
y5.2.35 <- Est(Ryukou5.2, 35)
y5.2.42 <- Est(Ryukou5.2, 42)
y5.2.42 <- Est(Ryukou5.2, 70)

y6.2.14 <- Est(Ryukou6.2, 14)
y6.2.21 <- Est(Ryukou6.2, 21)
y6.2.28 <- Est(Ryukou6.2, 28)
y6.2.33 <- Est(Ryukou6.2, 33)

パラメータ追加

peak <- c(100, 200, 300, 500, 1000, 3000, 4000, 5000, 6000, 7000, 10000, 30000, 50000)
mean <- c(44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 55, 60, 70)
sigma <- c(0.01, 0.05, 0.054, 0.055, 0.056, 0.057, 0.058, 0.059, 0.06, 1)

for(a in 1:length(peak)){
  for(b in 1:length(mean)){
    for(c in 1:length(sigma)){
      Prm <- rbind(Prm, c(peak[a], mean[b], sigma[c]))
    }
  }
}

head(Prm)
dim(Prm)

決定木のプログラム

決定木のプログラムメモ

library(rpart)
library(ROCR)

Data <- read.csv("...", as.is=T)

head(Data)
names(Data)
dim(Data)

tree01 <- rpart(Flag ~ ., data=Data, control=rpart.control(cp = 0.05))

par(mar=c(2, 2, 2, 2))
plot(tree01)
text(tree01, use.n = TRUE)
tree01

sink("...")
  tree01
sink()


#  木の性能チェック
pred <- 1 - predict(tree01)[1:nrow(Data)]
table(pred, Data$Flag)

prediction <- prediction(pred, factor(Data$Flag))
roc <- performance(prediction, "tpr", "fpr")


par(mar=c(3, 3, 3, 3))
plot(roc)

auc <- performance(prediction, "auc")
as.numeric(auc@y.values)

不均衡データのダウンサンプリングについて

論文や学術上では、不均衡データのときはダウンサンプリングしてデータを揃えたほうがいい、と言われるのが一般的かと思う。が、実際に分析をしてきた経験上、ダウンサンプリングすると特徴がうまく出ないことが多い。サンプリングせず、不均衡のままでモデルを作った方が正解データの特徴がはっきり出る。

そもそもダウンサンプリングすると予測力がどうなるのか？と気になって、Rで簡単なシミュレーションをしてみたところ、確かにダウンサンプリングしても予測力は変わらないし、特徴はちゃんと出た（詳細は下記）。ただ、実際のデータは変数が数千〜数万あったり、スパースだったりするので、サンプリングすることで特徴が出にくくなるのかもしれないと推察。スパースデータでのダウンサンプリングとかのテーマで研究もあるのかもしれない。あと、正解データの特徴が何パターンもあってサンプルサイズも多くないときは、非正解データをサンプリングすると特徴が出にくくなることもあるかも？（これもスパースなのが主な原因かな

サンプリングしない状態が真の状態であることは念頭に置きつつ、単純な特徴だとサンプリングしても大丈夫、サンプリングでうまく特徴が出なかったらサンプルサイズを増やしたりなるべくサンプリングせずに分析してみる、ということかな、といまのところは理解しておく。多重共線性も学術上はうるさく言われるけど実務上は気にすることはないし（共線性の影響が大きい重回帰はもうほとんど使わない）、学術と実務の違いなのかも。

※シミュレーション内容

・正解データ1,000

・非正解データ100,000

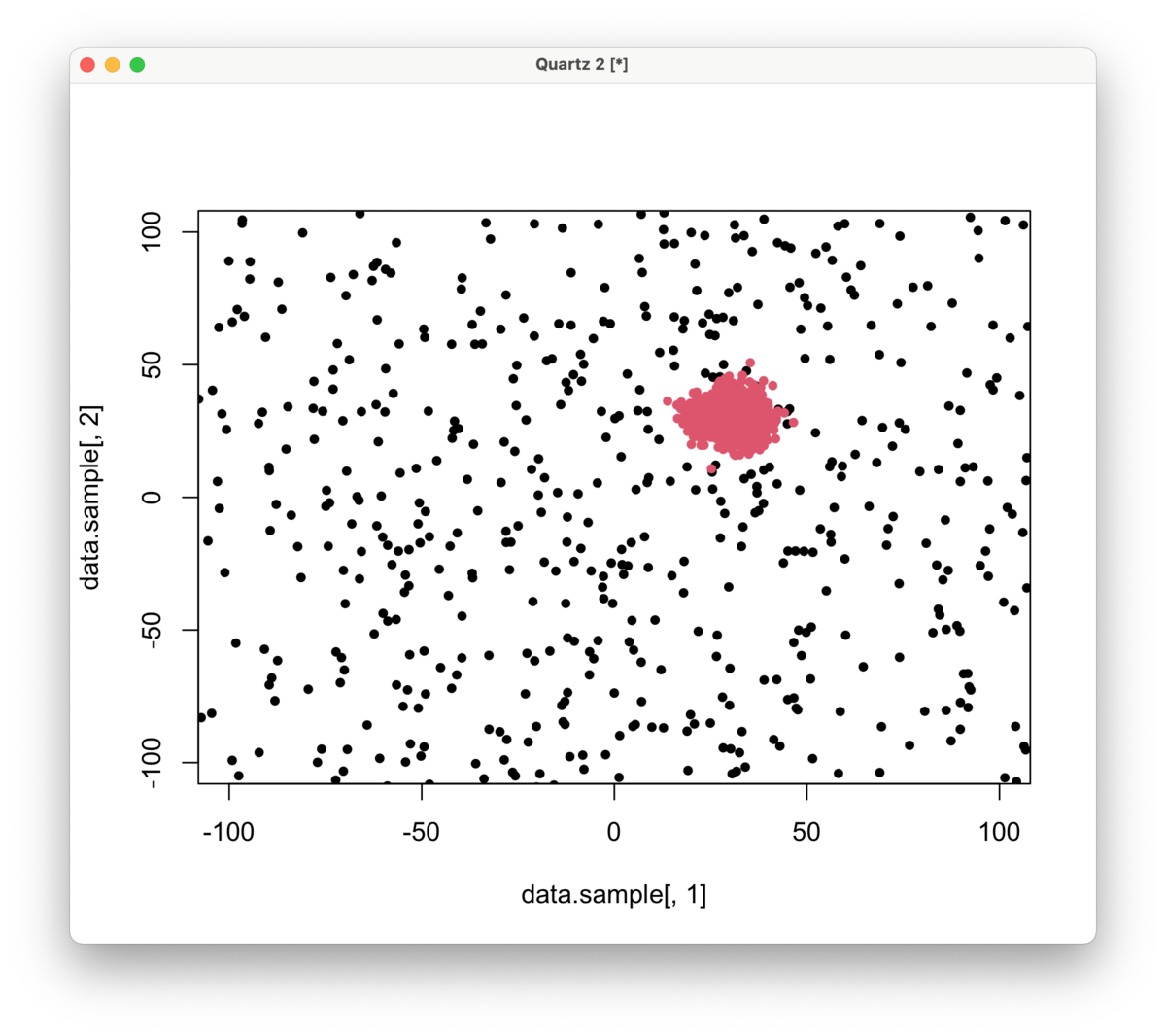
赤：正解データ

黒：非正解データ（1,000サンプリング）

サンプリングしない結果

AUC:0.9842543

1:1ダウンサンプリングした結果

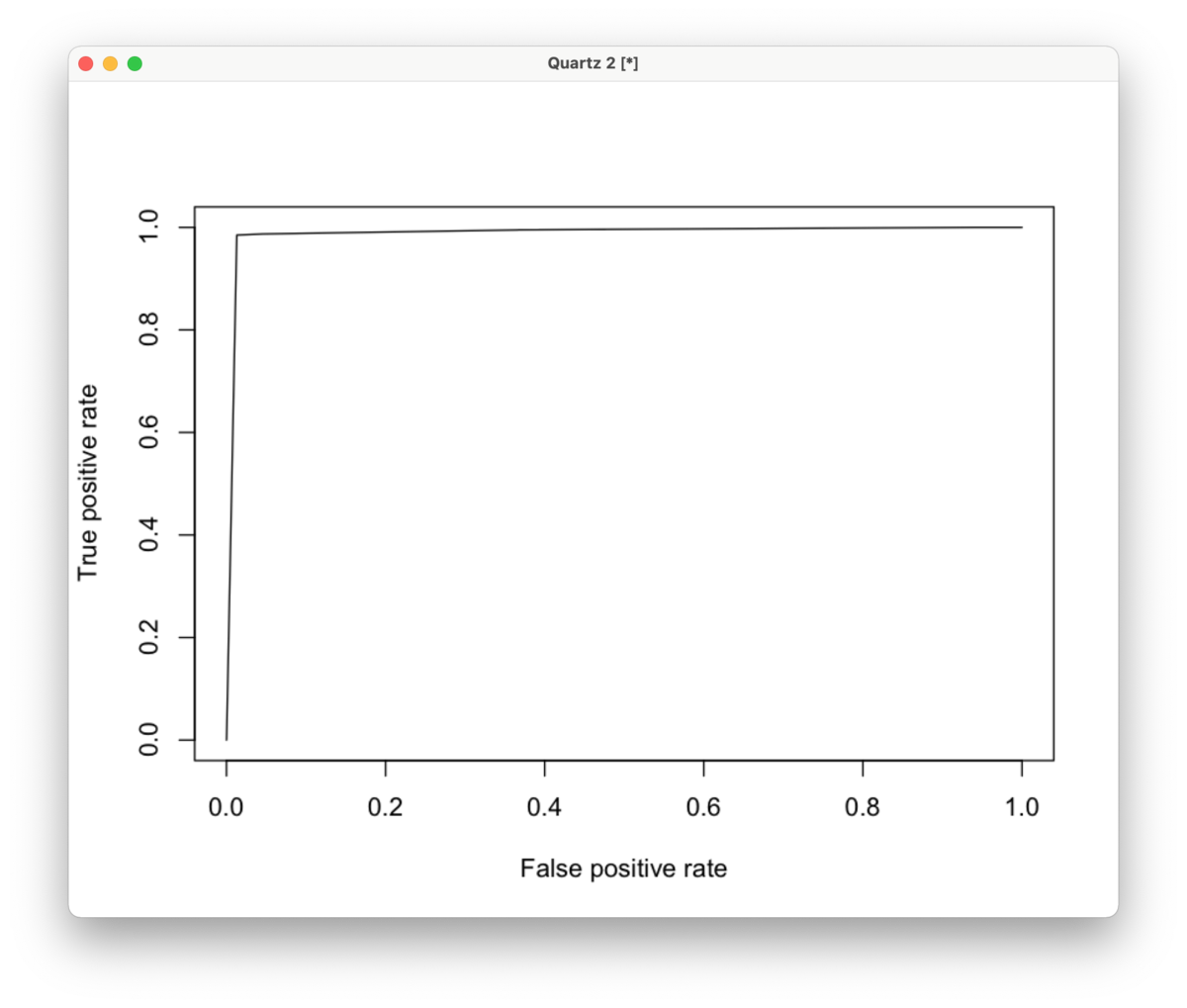
AUC:0.9886305

※下記Rコード

data1 <- cbind(x=rnorm(100000)*100, y=rnorm(100000)*100, flag=0)
data2 <- cbind(x=rnorm(1000)*5+30, y=rnorm(1000)*5+30, flag=1)

data <- rbind(data1, data2)

#plot(data[, 1], data[, 2], col=data[, 3]+1, pch=20, xlim=c(-100, 100), ylim=c(-100, 100))

library(rpart)
library(rpart.plot)
library(partykit)
library(ROCR)

tree <- rpart(factor(data[, 3]) ~ data[, 1] + data[, 2])

plot(tree)
text(tree, use.n = TRUE)

rpart.plot(tree)

plot(as.party(tree), gp=gpar(fontsize=9))

pred <- predict(tree)[(nrow(data)+1):(nrow(data)*2)]
pred1 <- prediction(pred, data[, 3])
perf <- performance(pred1,"tpr","fpr")
plot(perf)

auc.tmp <- performance(pred1,"auc")
auc <- as.numeric(auc.tmp@y.values)
auc

data.sample <- rbind(data1[sample(1:100000, 1000), ], data2)

#plot(data.sample[, 1], data.sample[, 2], col=data.sample[, 3]+1, pch=20, xlim=c(-100, 100), ylim=c(-100, 100))

tree.sample <- rpart(factor(data.sample[, 3]) ~ data.sample[, 1] + data.sample[, 2])
plot(as.party(tree.sample), gp=gpar(fontsize=9))

pred <- predict(tree.sample)[(nrow(data.sample)+1):(nrow(data.sample)*2)]
pred1 <- prediction(pred, data.sample[, 3])
perf <- performance(pred1,"tpr","fpr")
plot(perf)

auc.tmp <- performance(pred1,"auc")
auc <- as.numeric(auc.tmp@y.values)
auc